As simulation software and computer hardware have improved, analysts are focused on more lofty goals such as complex multiphysics analyses that previously could not be contemplated. A caveat is that analysts of today need not be as concerned with efficient computer solution times or memory issues, and therefore spend less time doing things like optimizing the mesh, defeaturing models, and simplifying loading conditions unless they’re dealing with highly complex runs. The analysts of 30 years ago were faced with different challenges than those of today as they worked to solve the same problems. Along the way some basic analysis expertise may have been unfortunately lost, or thankfully left behind.
For example, years ago the simultaneous equations from the FEA formulation were solved only by a wavefront-type solver. This required careful ordering of the elements so that degrees of freedom could be Gaussian-eliminated along the way. This was a painful step that required expertise, which thankfully, is no longer needed. Substructuring (Guyan Reduction) and submodeling are other techniques that are used less often these days, but still have a place in today’s complex analyses. These topics will be touched upon in a separate blogs. Today we’re talking about the judicious use of symmetry conditions, which can be used to greatly reduce solution time without loss of accuracy. It’s commonly used by analysts today, but warrants a reminder here since it can be overlooked by those consumed with the more lofty goals, and equipped with powerful multiprocessing computers.
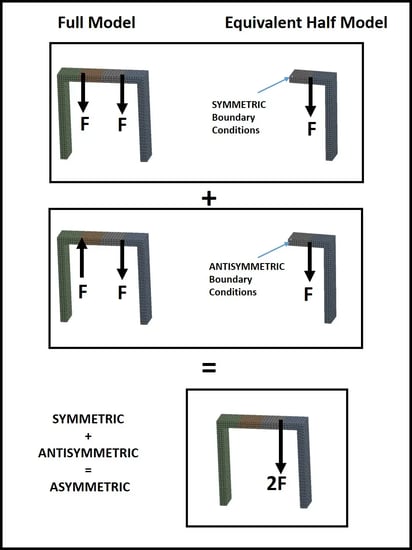
Symmetry allows the model to be reduced to one-half size resulting in a dramatic reduction in computer time, or the enabling of a much higher mesh density for better accuracy. When talking symmetry in the context of an FEA model, both the geometry and the loading must be considered. If both the loads and the geometry on one side of the model are a mirror image of the other side, then symmetric boundary conditions would need to be applied to a one-half model at the mirror/cut plane. If the geometry is a mirror image, but the loading on the other side of the mirror/cut plane is of equal magnitude but flipped in sign, then antisymmetric boundary conditions must be applied to the mirror plane. An extension of this, that may not be obvious to all, is that these two load conditions can be combined to create asymmetric loading conditions. As depicted below, adding these two load cases together cancels out the load on the left and doubles the load on the right. Subtracting the load cases does the opposite. So a one-half model can be used for the asymmetric case where no load is applied to the other half. Scale factors can be applied before adding or subtracting load cases also.
 |
 |
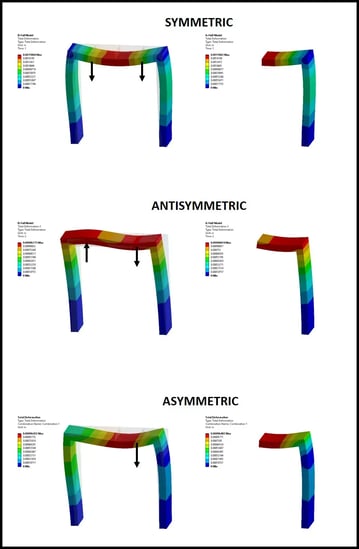Modern software codes apply symmetry boundary conditions automatically when calling out a specific surface as a mirror plane. However, analysts should know how to manually constrain degrees of freedom at the symmetry plane. In ANSYS Workbench, for example, you cannot switch between symmetric and antisymmetric conditions from one load step to another unless you apply them as displacement constraints. For a symmetric boundary condition, the translational DOF normal to the mirror plane is constrained, along with the two rotations about the other two DOFs. For antisymmetry, the opposite three DOFs are constrained. For solid elements, with no rotational DOFs, of course only the translations come into play.
Symmetric Structure with Asymmetric Loading
Make sure to take the opportunity to make your models runs more efficiently by exploiting symmetry. There is no downside, only faster run times, more accuracy, or both. In some cases the one-half model can be expanded to a full model for post-processing images of the entire model. Be aware that there are limitations to the use of these techniques for models with nonlinearities. Also, note that cyclic symmetry is a bit different and warrants its own discussion. Basically, it exploits repeatable sector models which are subjected to specific load variation from sector to sector.
Interested in exploring more about our FEA capabilities?
